Other Placeholder: 10
Ejercicio
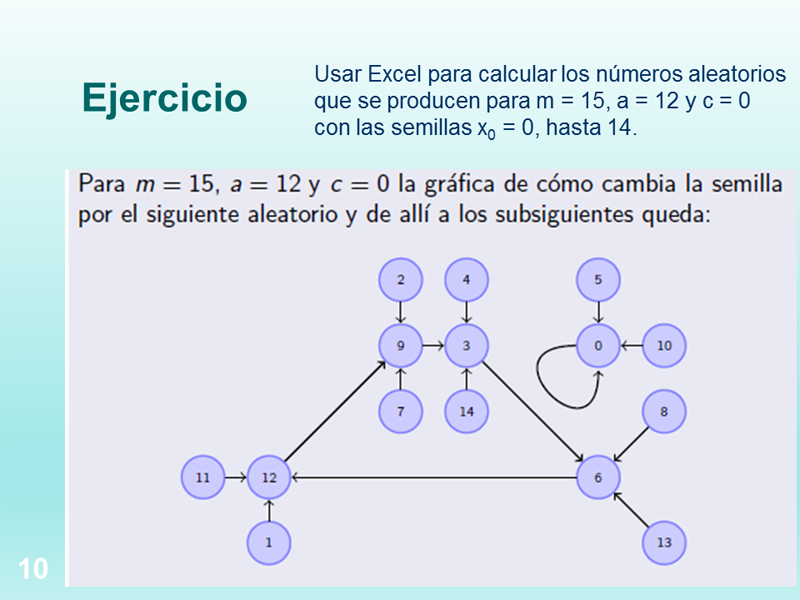
Usar Excel para calcular los números aleatorios que se producen para m = 15, a = 12 y c = 0 con las semillas x0 = 0, hasta 14.

Title: GCL Multiplicativos
Other Placeholder: 11
Periodo completo = Cuando tiene el máximo periodo posible, m – 1.
Los hay con m potencia de 2 (m = 2k ) que son rápidos pues el residuo en divisiones con potencia de 2 puede hacerse rápidamente. Aunque tienen la desventaja que no son de periodo completo pueden ser suficientes para muchas aplicaciones.
Cuando m no es potencia de 2 el generador es menos rápido; se acostumbra elegir un número m que sea primo y la relación entre m y a debe ser especial para que el generador tenga un periodo completo o al menos grande.

Other Placeholder: 12

Other Placeholder: 13

Title: Ejercicio 2
Other Placeholder: 14
Suponiendo que se utilice el generador de números seudo-aleatorios.
y que la semilla se escoge eligiendo al azar un entero entre 1 y 26 – 1 inclusive, determine el promedio de la longitud del periodo y su desviación estándar.

Other Placeholder: 15
Varianza:
Desviación Estándar:
Varianza y Desviación Estándar para una muestra de datos.

Other Placeholder: 16
1. Determina el rango, la varianza y la desviación estándar para los siguientes datos:
2 4 3 5 2 2 0 1
R = Rango 5; Varianza 2.5536 y Desviación Estándar 1.5980
2. Determina el rango, la varianza y la desviación estándar para los siguientes datos:
-2 -4 -3 -5 -2 -2 0 -1
R = Rango 5; Varianza 2.5536 y Desviación Estándar 1.5980
3. Determina el rango, la varianza y la desviación estándar para los siguientes datos:
6 12 9 15 6 6 0 3
R = Rango 15; Varianza 22.9821 y Desviación Estándar 4.7940
Ejercicio

Other Placeholder: 17
Frecuentemente se utilizan generadores de números seudo-aleatorios en forma encadenada; por ejemplo, el número que sale de
xn+1 = (81 ·xn + 121) mod 255
es utilizado por
yn+1 = (625 · xn+1 + 48) mod 63
para producir el número yn+1 que es el que se reporta.
Usando la semilla x0 = 23 y los datos anteriores, determine los primeros 2 números aleatorios generados (y1 y y2).
Ejercicio

Other Placeholder: 18
Frecuentemente se utilizan generadores de números seudo-aleatorios en forma encadenada; por ejemplo, el número que sale de
xn+1 = (45 ·xn + 71) mod 127
es utilizado por
yn+1 = (125 · xn+1 + 11) mod 63
para producir el número yn+1 que es el que se reporta.
Usando la semilla x0 = 49 y los datos anteriores, determine los primeros 2 números aleatorios generados (y1 y y2).
Otro ejercicio

Title: Probando generadores de números aleatorios
Other Placeholder: 19
Es importante asegurarse de que el generador usado produzca una secuencia suficientemente aleatoria. Para esto se somete el generador a pruebas estadísticas. Si no pasa una prueba, podemos asumir que el generador es malo. Pasar una prueba es una condición necesaria pero no suficiente. Un generador puede pasar una prueba y luego no pasarla si se usa otra semilla u otro segmento del ciclo.

Other Placeholder: 20
¿Cómo sabemos que nuestro generador es bueno?
PRUEBAS GRÁFICAS
Gráfica de Serie de Tiempo.
Tablas de frecuencias e histogramas
PRUEBA ESTADÍSTICA
Prueba Ji-cuadrada
Usar el ejemplo: xn+1 = (75 ·xn) mod 231 – 1
Con semilla = 1, los primeros 200 números generados.

Title: Gráfica de Serie de Tiempo
Other Placeholder: 21
Es importante observar que NO exista ningún patrón o tendencia.
xn+1 = (75 ·xn) mod 231 – 1
Con semilla = 1, los primeros 200 números generados

Other Placeholder: 22
¿Cómo sabemos que nuestro generador es bueno?
¿Cuál de estas series de números parecen venir de un buen generador?

Other Placeholder: 23
Tabla de frecuencias e histograma

Other Placeholder: 24
(Gp:) 0, x < 0
F(x) = x, 0 ? x ? 1
1, x
 Página anterior Página anterior |   Volver al principio del trabajo Volver al principio del trabajo | Página siguiente  |